Introduction
Graph Neural Networks (GNN) is one of the trending topics among AI researchers and scientists, and it has the unique ability to solve real-world problems using graph data.
I will explain how Graph Neural Network works, The History of Graph Neural Networks, Types of Graph Neural Networks, a Brief overview of Graph Convolutional Networks and Applications of Graph Neural Networks.
First, let’s discuss graph data a bit.
Graph Data
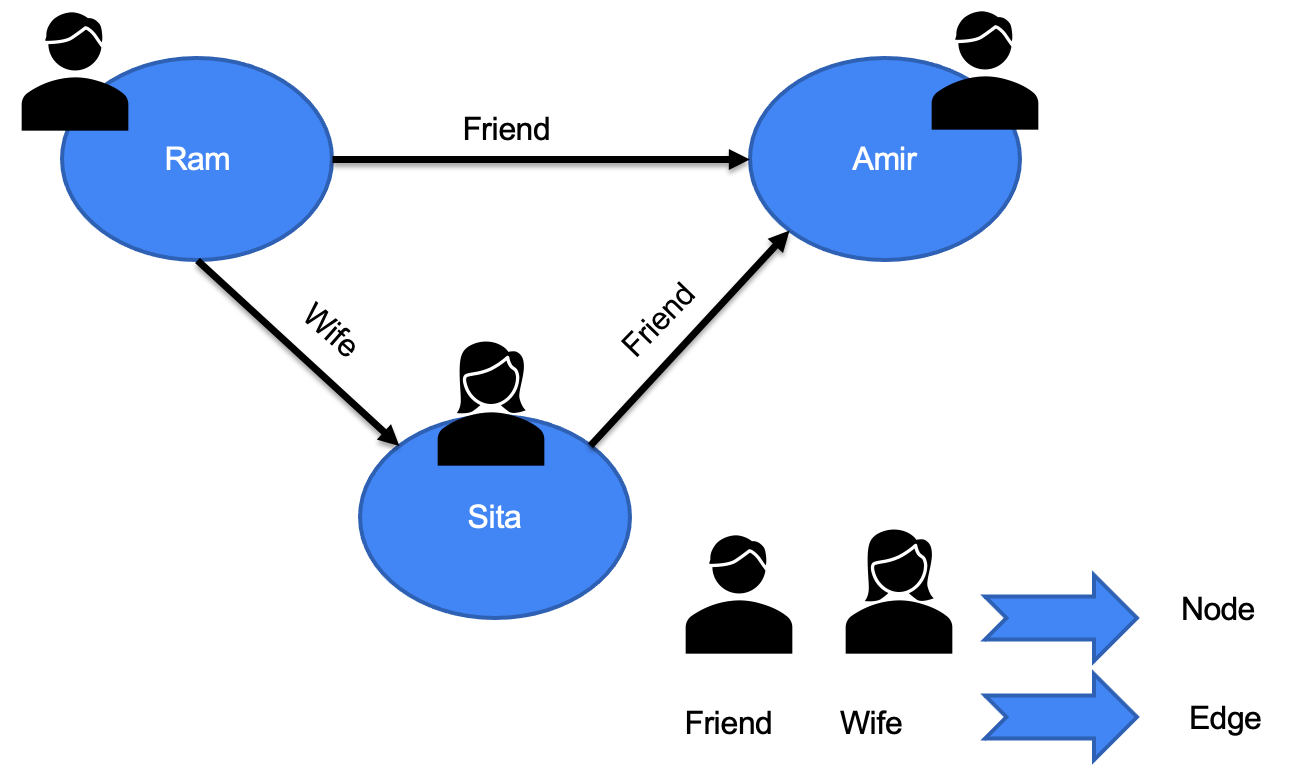
Graph data is a way of organising and representing data in nodes (also called vertices) and edges (also called Links). The nodes represent individual objects or entities, and the edges represent their connections or relationships.
Examples:
Let’s think of a social network like Facebook, where each user (Ram, Amir, Sita) is a node, and each connection between users (such as a friendship, Wife) is an edge.
Let’s consider Movie Graph data, where Nodes are the individual Movie and People, such as (Journey, Roopesh, Tom, Ali, Jack, Yu and Tom Cruz), and the edges are the relationship between them, such as (Acted in and Directed by)
Let’s consider a Transport Navigation graph data where nodes are the Travel destinations such as (Times Square NYC, New Jersey and Boston). Edges are the ( Estimated Travel Time, Speed limit, Traffic, Mode of transport and Distance).
Let’s consider a Chemical reactions graph data between atoms, where individual atoms such as (Carbon, Hydrogen, Sulfur, Nitrogen and Oxygen) are nodes and their different types of bonds such as the (Double covalent bond, Hydrogen bond, Electro Negativity bond and Covalent bond) are the edges.
These nodes and edges can be represented in a graph as points and lines.
In recent years, the use of graph data has increased in areas such as machine learning and data science, where graph-based models and algorithms are used to analyse and make predictions based on complex relationships such as the spread of a disease through a social network, the flow of traffic through a transportation network, or the interactions between proteins in a biological network.
Graph Neural Network algorithms and models can be used to extract insights and make predictions based on these complex relationships between entities.
History of Graph Neural Networks
Graph neural networks (GNNs) have their roots in the field of artificial neural networks (ANNs) in the 1940s. However, the specific idea of using neural networks to model complex graph-structured data emerged more recently in the late 2000s
In 2009, a paper Titled “The Graph Neural Network Model” introduced a novel neural network architecture based on a recursive message-passing scheme.
Where each node in the graph aggregates messages from its neighbouring nodes and then applies a nonlinear transformation to the aggregated messages to compute its hidden representation
The resulting hidden representations of all nodes in the graph are then passed through a readout function to produce the final output. This paper can be viewed as a precursor to modern graph neural networks (GNNs) as there, the authors proposed a novel neural network architecture that operates directly on graph-structured data.
Graph Neural Networks Types Explained
Post 2010, there was a paradigm shift in graph neural networks, which brought us several innovative papers that contributed to the development of graph neural networks.
Let’s look at graph neural networks classified papers,
In 2016, Graph Auto Encoders was published, and in 2017, Graph Convolution Networks was published. In 2018, contributed to 3 major papers, such as Graph Attention Nets, Graph Recurrent Neural Networks, and Graph Convolution LSTM Networks and in 2019, Graph Transformers Networks was published. Graph Auto Encoders.
Let’s briefly discuss the types of graph neural networks and their use cases.
Graph Auto Encoders (GAEs):
GAEs are used for unsupervised learning on graph-structured data. They try to learn a compressed graph representation that can be used to reconstruct the original graph.
Graph Autoencoders can be used for tasks such as anomaly detection and network visualisation. Link to Paper
Graph Convolutional Networks (GCNs):
Graph Convolutional Networks use a convolutional graph operation to aggregate information from a node's neighbours and generate a new representation for that node.
This operation can be applied to multiple neural network layers to learn increasingly complex representations.
This can be used for tasks such as Node Classification, Link Prediction, and Graph Generation. Link to Paper
Graph Attention Networks (GATs):
Graph Attention Networks use an attention mechanism to weigh the contributions of each node's neighbours when computing the new representation for that node. This allows the network to focus on the most relevant information for each node rather than treating all neighbours equally.
Graph Attention Networks are also used for tasks such as Node Classification, Link Prediction, Graph Generation, Semi-supervised learning, knowledge graph and Community detection. Link to Paper
Graph Recurrent Neural Networks (GRNNs):
In Graph Recurrent Neural Networks, the graph is traversed in a sequence of node visits. At each visit, the representation of each node is updated based on its previous representation and those of its neighbours.
Graph Recurrent Neural Networks have been applied to various tasks involving graph-structured data, including node classification, link prediction, and graph generation. Link to Paper
Graph Convolutional LSTM Networks
The Graph Convolutional LSTM Networks combine graph convolutional operations with recurrent neural network (RNN) operations to process graph-structured data.
However, there is a difference in the specific type of RNN used in each approach. Graph Recurrent Neural Networks use a standard RNN architecture, whereas Graph Convolutional LSTM Networks use a Long Short-Term Memory (LSTM) architecture, which is a variant of the RNN.
LSTMs are designed to address the vanishing gradient problem that can occur in standard RNNs by using a memory cell and Gating mechanisms that control the flow of information through the network.
This can make GC-LSTM Networks better suited for modelling longer-term dependencies in the graph data.
Both GCRNs and GC-LSTM Networks have been shown to be effective for graph-based tasks such as node classification, link prediction and graph generation.
The choice between the two approaches may depend on the specific characteristics of the dataset and the task at hand. Link to Paper
Graph Transformer Network
Graph Transformer Networks (GTNs) are a type of Graph Neural Network (GNN) that uses the Transformer architecture to process graph-structured data.
Transformers were originally developed for natural language processing tasks and have since been applied to a wide range of other domains, including computer vision and speech recognition. Link to Paper
Graph Convolutional Networks (GCNNs)
Graph Convolutional Networks (GCNNs) are a type of neural network that can operate on graph-structured data. The below image is an example of how the GCN is being done.
GCNNs are inspired by the success of Convolutional neural Networks (CNNs) in image processing tasks, and they extend CNNs to work with non-Euclidean data structures like graphs. The key idea in Graph Convolutional Neural Networks is to define convolutional filters that operate on the graph structure.
These filters can be applied to the nodes in the graph, taking into account their neighbours and their respective edge weights. The output of the convolutional filter is a transformed version of the node's feature vector.
GCN Aggregation
Let's understand how the Aggregation of the input Graph is computed,
From the example aggregate function, the input graph data has 6 nodes in the range from 1 to 6, and it has connected edges between them.
Let’s take Target Node 4,
Look how the computation graph is being done.
Target 4 defines a computation graph. Each edge is connected directly to target 4 and transforms into an aggregate function; likewise, each node represents its computation graph, and each edge in the graph is an Aggregation.
In Layman's Terms,
In the input graph, let’s look at Target Node 4 and, which has three direct nodes connected to it, 3, 5, 6, respectively, which transforms to an aggregation and further, this, 3,5,6 Nodes, each connected node of 3, such as the 1,2,4 are transformed to an aggregation function respectively. Likewise, Node 5 and Node 6’s directly connected nodes are further transformed into an aggregation function.
How is Aggregation computed technically?
Let’s get a bit deep into the aggregation and the resulting feature vector of graph convolution Networks.
For each node in the graph, its feature vector is first transformed using a learned weight matrix.
Then, the transformed feature vectors of the node's neighbours are aggregated by computing a weighted sum.
Generally, the weights are determined by the edge weights of the graph and can be computed using a SoftMax function to ensure that they sum up to 1.
Later, the aggregated feature vector is then passed through a non-linear activation function, such as the rectified linear unit (ReLU).
Finally, The resulting feature vector is the output of the graph convolutional layer for that node.
The above process can be repeated for multiple layers of neural networks to capture more complex graph features.
In each layer, the feature vectors of the nodes are updated based on the feature vectors of their neighbours, which allows the network to capture the local and global structure of the graph.
Aggregation is a crucial part of GCNs, enabling the network to capture the relationships between the nodes in the graph.
Advantage and Use Case
One advantage of GCNNs is that they can operate on graphs of arbitrary size and structure, making them applicable to solve a wide range of problems.
GCNNs have been applied to various tasks involving graph-structured data, including node classification, link prediction, and graph classification. They have shown promising results in several domains, including social, biological, and citation networks.
Challenges of GCN
The design of the convolutional filters and the choice of hyperparameters can be a challenging task in Graph Convolution Networks.
The choice of filter size, depth, and number of features can significantly impact the performance of the GCN.
The design of the convolutional filters is problem-specific. and requires domain knowledge to define meaningful filters that capture relevant features of the graph.
Another challenge of GCNNs is their computational complexity, which can be high for large graphs.
The computation of the adjacency matrix and the multiplication with the weighted matrix can be expensive, especially for dense graphs.
Overcoming Challenges
Several techniques have been proposed to address this issue, including graph sparsification and parallelisation.
One technique to address these challenges is graph sparsification, which involves reducing the number of edges in the graph while preserving its structural properties. This can make the computation more efficient and allow for the use of larger graphs. Another approach is parallelisation, where the computation is distributed across multiple processing units to speed up the training process.
Despite these challenges, GCNNs have shown promising results in various applications, such as social network analysis, recommendation systems, and bioinformatics. Researchers are actively working on improving the efficiency and scalability of GCNNs and exploring new architectures and applications. Overall, GCNNs are an exciting area of research in the machine-learning community.
Difference between Native ML Lifecycle vs Graph Neural Network Lifecycle
● In the Traditional machine learning Model Lifecycle,
which require domain expertise and extensive feature engineering to extract relevant features from raw input data. And then, the model prediction is done for deployment.
In contrast, GNNs can automatically learn representations of nodes and edges from raw input graph data. This is especially useful in scenarios where the graph structure is complex and difficult to model manually. GNNs can learn features specific to the particular graph structure, which can capture the interactions between nodes and edges more accurately.
Moreover, GNNs can handle various types of input data, including graphs with different structures, sizes, and characteristics. They can learn from the input data and capture the underlying patterns and relationships without requiring any prior knowledge about the data or the graph structure. This makes GNNs more versatile and adaptable to different use cases and applications.
Overall, the ability of GNNs to learn from raw graph data without requiring extensive feature engineering is a significant advantage that can save time and effort and improve the accuracy and performance of the models.
Stay tuned for the upcoming educational series of GCN !!!
Industrial Application Use-cases and Live Code Implementations.
COMING SOON….!!!!

References
SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS
Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering
Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting: